


















Johann Jakob Balmer (1 de mayo de 1825 – 12 de marzo de 1898) fue un matemático suizo y físico honorario, autor de la fórmula que lleva su nombre, la cual permite obtener los números de onda de la serie espectral del átomo de hidrógeno.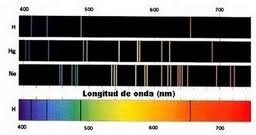
Fue el mayor de los hijos de Johann Balmer -Presidente del Tribunal Supremo- y Elisbeth RolleBalmer;asistió a la escuela de primaria en Liestal, un pueblo que acababa de convertirse en la capital del cantón de Basilea-Landschaft. En Basilea, continuó con la educación secundaria, donde fue un alumno destacado en matemáticas, conitnuando con estos estudios en la Universidad.
Estudió en la Universidad de Karlsruhe y en la Universidad de Berlín, luego completó su carrera como Doctor en Filosofía de la Universidad de Basilea en 1849 con una disertación sobre la cicloide. Johann entonces pasó su vida entera en Basilea, donde dió clases en una escuela femenina. En 1868 se casó con Christine Pauline Rinck a la edad de 43 años. La pareja tuvo un total de seis hijos.
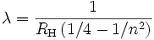 A pesar de ser un profesor de matemáticas durante toda su vida, Balmer es más recordado por su trabajo en la serie espectral y su fórmula para las longitudes de onda de las líneas espectrales del átomo se hidrógeno. Quedó reflejado en los dos únicos artículos que escribió sobre los espectros de los elementos en 1855 y en 1867, respectivamente.
A pesar de ser un profesor de matemáticas durante toda su vida, Balmer es más recordado por su trabajo en la serie espectral y su fórmula para las longitudes de onda de las líneas espectrales del átomo se hidrógeno. Quedó reflejado en los dos únicos artículos que escribió sobre los espectros de los elementos en 1855 y en 1867, respectivamente.
La mayor contribución que hizo Balmer, dependía mucho más de sus conocimientos matemáticos que de su comprensión de la física, ya que crea una fórmula que dió a las longitudes de onda de las líneas observadas producidas por el átomo de hidrógeno, sin dar una explicación física. La famosa fórmula de Balmer es: λ = hm 2 / (m 2 - n 2). Teniendo en cuenta que n = 2 y h = 3654,6 x 10 -8 cm, las longitudes de onda dadas por la fórmula para m = 3, 4, 5, 6 eran correctas a un alto grado de precisión. Los intentos anteriores habían buscado fórmulas de tipos muy diferentes y no ocurrió nada que concuerde con la evidencia experimental. Poniendo m = 7 dió Balmer un valor de predicción para la siguiente línea y, de hecho un colega de la Universidad de Basilea fue capaz de decirle a Balmer que esta línea y la longitud de onda había sido observada de acuerdo a un alto nivel de precisión con la fórmula de Balmer una predijo.
hecho un colega de la Universidad de Basilea fue capaz de decirle a Balmer que esta línea y la longitud de onda había sido observada de acuerdo a un alto nivel de precisión con la fórmula de Balmer una predijo.
En su artículo de 1885 Balmer sugirió que dar n otros valores enteros pequeños daría a las longitudes de onda de otra serie producida por el átomo de hidrógeno. De hecho esta predicción resultó ser correcta y esta serie de líneas se observaron más tarde. La razón por la cual la fórmula es válida no se entendía en la vida de Balmer y tuvo que esperar hasta el trabajo teórico de Niels Bohr en 1913.
