


















Abraham de Moivre, matemático británico de origen francés, de Moivre nació en Vitry-le-François, Champagne, Francia el 26 de mayo de 1667 y murió en Londres el 27 de noviembrede 1754.
Aunque su padre era cirujano, su familia no era rica. De religión protestante, sin embargo sus primeras enseñanzas las tuvo en una escuela católica, en Vitry. Después, con 11 años fue a una academia protestante en Sedan, donde pasó 4 años aptrendiendo griego.
Esta academia fue suprimida por el gobierno francés en 1682. De Moivre fue entonces a Saumur donde estudió lógica hasta 1684. En esta época estudió matemáticas por su cuenta, leyéndose un tratado de Huygens. Al mudarse sus padres a Paris, Abraham pasa al Collège de Harcourt, donde estudia física y matemáticas.
En 1685, Louis XIV revoca el edicto de Nantes y comienza la persecución religiosa a los protestantes. Se produce la expulsión de los hugonotes. De Moivre marcha a Londres, donde se convierte en instructor privado de matemáticas. Enseñando también en los cafés.
En esa época estudia los Principia de Newton, libro recién publicado e intenta sin éxito obtener una plaza de profesor de matemáticas edn alguna universidad. Sin embargo, sus investigaciones si tienen éxito, conoce personalmente a Newton. En marzo de 1695, Halley comunica su primer artículo titulado Method of fluxions a la Royal Society. Siendo elegido, en 1697, miembre de dicha sociedad.
En 1710, de Moivre fue designado, por ser amigo de Newton, para la comisión de la Royal Society que debía estudiar las reclamaciones de Leibniz como descubridor del cálculo antes que Newton. Así la Royal Society obtuvo la respuesta que esperaba.
 De Moivre fue pionero en el desarrollo de la geometría analítica y de la teoría de probabilidades. En 1718, publicó su libro The Doctrine of Chance: A method of calculating the probabilities of events in play. En 1711, ya había publicado una versión en latín en la revista Philosophical Transactions. La definición de independencia estadística aparece en este libro junto con problemas de dados y juegos.
De Moivre fue pionero en el desarrollo de la geometría analítica y de la teoría de probabilidades. En 1718, publicó su libro The Doctrine of Chance: A method of calculating the probabilities of events in play. En 1711, ya había publicado una versión en latín en la revista Philosophical Transactions. La definición de independencia estadística aparece en este libro junto con problemas de dados y juegos.
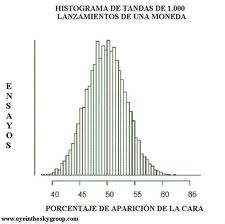
En su trabajo, Miscellanea Analytica de 1730, ya aparece la llamada erróneamente fórmula de Stirling, que usó posteriormente en 1733 para derivar la curva normal como una aproximación a la distribución binomial. La atribución errónea quizás sea debida a que en la segunda edición del libro en 1738, de Moivre da crédito a Stirling por una mejora de la fórmula.
De Moivre es recordado por la fórmula que ya usó en 1707: ei n x = (cos x + i sin x)n
La cual introdujo la Trigonometría en el análisis, y que fué importante en el desarrollo de la aritmética de los números complejos.
También, en su obra Miscellanea analytica, publicada en Londres en 1730, aparece por vez primera la solución general de una ecuación lineal en recurrecia. Obteniendo mucho antes que Binet, la hoy errónamente llamada fórmula de Binet para obtener el término n-ésimo de la sucesión de Fibonacci:
![]()
En 1754, fue elegido miembro de la Academia de Ciencias de Paris. A pesar de su indiscutiblle categoría científica y su amistad con Newton y Leibniz, de Moivre nunca consigió una plaza en ninguna universidad. Nunca se casó, era un ferviente cristiano. Fue siempre instructor privado de matemáticas y murió en la pobreza.
